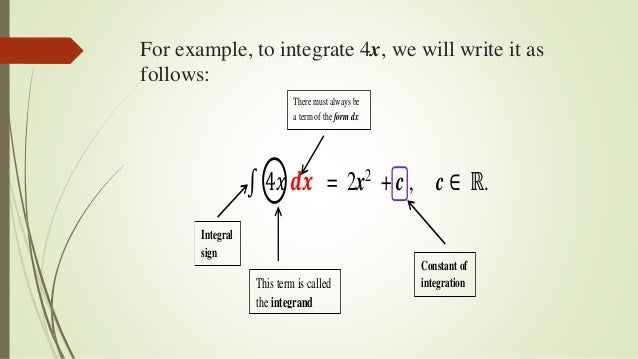
annalg.blogg.se - Integral in calculus examples

#Integral in calculus examples how to

METHOD OF SUBSTITUTION (CHANGE OF VARIABLE) Note: In the answer for all integral sums we add +c (constant of integration) since the differentiation of constant is always zero.Įxamples: Evaluate the following integral: Integral calculus was primarily invented to determine the area bounded by the curves dividing the entire area into infinite number of infinitesimal small areas and taking the sum of all these small areas. Hence and this c is called the constant of integration Thus if we differentiate we can get back x n.Īgain if we differentiate and c being a constant, we get back the same x n Integral of xn with respect to variable x is equal to Hence, from equation (1), it follows that Integration is the inverse operation of differentiation and is denoted by the symbol . And sometimes we have to divide up the integral if the functions cross over each other in the integration interval.Integration is the reverse process of differentiation. Note that we may need to find out where the two curves intersect (and where they intersect the \(x\)-axis) to get the limits of integration. The cool thing about this is it even works if one of the curves is below the \(x\)-axis, as long as the higher curve always stays above the lower curve in the integration interval.

#Integral in calculus examples how to

Since we know how to get the area under a curve here in the Definite Integrals section, we can also get the area between two curves by subtracting the bottom curve from the top curve everywhere where the top curve is higher than the bottom curve. Since we already know that can use the integral to get the area between the \(x\)- and \(y\)-axis and a function, we can also get the volume of this figure by rotating the figure around either one of the axes. One very useful application of Integration is finding the area and volume of “curved” figures, that we couldn’t typically get without using Calculus.

Applications of Integration: Area and VolumeĪrea Between Curves Volumes of Solids: The Washer Method Volumes of Solids by Cross Sections Volumes of Solids: The Shell Method Volumes of Solids: The Disk Method More Practice.

Exponential and Logarithmic Integration.

Riemann Sums and Area by Limit Definition.

Differential Equations and Slope Fields.

Antiderivatives and Indefinite Integration, including Trig.

Derivatives and Integrals of Inverse Trig Functions.

Exponential and Logarithmic Differentiation.

Differentials, Linear Approximation, Error Propagation.

Curve Sketching, Rolle’s Theorem, Mean Value Theorem.

Implicit Differentiation and Related Rates.

Equation of the Tangent Line, Rates of Change.

Differential Calculus Quick Study Guide.

Polar Coordinates, Equations, and Graphs.Law of Sines and Cosines, and Areas of Triangles.Linear, Angular Speeds, Area of Sectors, Length of Arcs.Conics: Circles, Parabolas, Ellipses, Hyperbolas.Graphing and Finding Roots of Polynomial Functions.Graphing Rational Functions, including Asymptotes.Rational Functions, Equations, and Inequalities.Solving Systems using Reduced Row Echelon Form.The Matrix and Solving Systems with Matrices.Advanced Functions: Compositions, Even/Odd, Extrema.Solving Radical Equations and Inequalities.Solving Absolute Value Equations and Inequalities.

Imaginary (Non-Real) and Complex Numbers.Solving Quadratics, Factoring, Completing Square.Introduction to Multiplying Polynomials.Scatter Plots, Correlation, and Regression.Algebraic Functions, including Domain and Range.Systems of Linear Equations and Word Problems.Introduction to the Graphing Display Calculator (GDC).Direct, Inverse, Joint and Combined Variation.Coordinate System, Graphing Lines, Inequalities.Types of Numbers and Algebraic Properties.Introduction to Statistics and Probability.Powers, Exponents, Radicals, Scientific Notation.